x=.9999...
10x=9.9999...
Subtract x from both sides
9x=9
x=1
There it is, folks.
Somehow I have the feeling that this is not going to convince people who think that 0.9999... /= 1, but only make them madder.
Personally I like to point to the difference, or rather non-difference, between 0.333... and ⅓, then ask them what multiplying each by 3 is.
I was taught that if 0.9999... didn't equal 1 there would have to be a number that exists between the two. Since there isn't, then 0.9999...=1
Divide 1 by 3: 1÷3=0.3333...
Multiply the result by 3 reverting the operation: 0.3333... x 3 = 0.9999.... or just 1
0.9999... = 1
Okay, but it equals one.
No, it equals 0.999...
2/9 = 0.222... 7/9 = 0.777...
0.222... + 0.777... = 0.999... 2/9 + 7/9 = 1
0.999... = 1
No, it equals 1.
Similarly, 1/3 = 0.3333…
So 3 times 1/3 = 0.9999… but also 3/3 = 1
Another nice one:
Let x = 0.9999… (multiply both sides by 10)
10x = 9.99999… (substitute 0.9999… = x)
10x = 9 + x (subtract x from both sides)
9x = 9 (divide both sides by 9)
x = 1
My favorite thing about this argument is that not only are you right, but you can prove it with math.
That's the best explanation of this I've ever seen, thank you!
That's more convoluted than the 1/3, 2/3, 3/3 thing.
3/3 = 0.99999...
3/3 = 1
If somebody still wants to argue after that, don't bother.
Sure, when you start decoupling the numbers from their actual values. The only thing this proves is that the fraction-to-decimal conversion is inaccurate. Your floating points (and for that matter, our mathematical model) don't have enough precision to appropriately model what the value of 7/9 actually is. The variation is negligible though, and that's the core of this, is the variation off what it actually is is so small as to be insignificant and, really undefinable to us - but that doesn't actually matter in practice, so we just ignore it or convert it. But at the end of the day 0.999... does not equal 1. A number which is not 1 is not equal to 1. That would be absurd. We're just bad at converting fractions in our current mathematical understanding.
Edit: wow, this has proven HIGHLY unpopular, probably because it's apparently incorrect. See below for about a dozen people educating me on math I've never heard of. The "intuitive" explanation on the Wikipedia page for this makes zero sense to me largely because I don't understand how and why a repeating decimal can be considered a real number. But I'll leave that to the math nerds and shut my mouth on the subject.
You are just wrong.
The rigorous explanation for why 0.999...=1 is that 0.999... represents a geometric series of the form 9/10+9/10^2+... by definition, i.e. this is what that notation literally means. The sum of this series follows by taking the limit of the corresponding partial sums of this series (see here) which happens to evaluate to 1 in the particular case of 0.999... this step is by definition of a convergent infinite series.
The only thing this proves is that the fraction-to-decimal conversion is inaccurate.
No number is getting converted, it's the same number in both cases but written in a different representation. 4 is also the same number as IV, no conversion going on it's still the natural number elsewhere written S(S(S(S(Z)))). Also decimal representation isn't inaccurate, it just happens to have multiple valid representations for the same number.
A number which is not 1 is not equal to 1.
Good then that 0.999... and 1 are not numbers, but representations.
It still equals 1, you can prove it without using fractions:
x = 0.999...
10x = 9.999...
10x = 9 + 0.999...
10x = 9 + x
9x = 9
x = 1
There's even a Wikipedia page on the subject
I hate this because you have to subtract .99999..... from 10. Which is just the same as saying 10 - .99999.... = 9
Which is the whole controversy but you made it complicated.
It would be better just to have them do the long subtraction
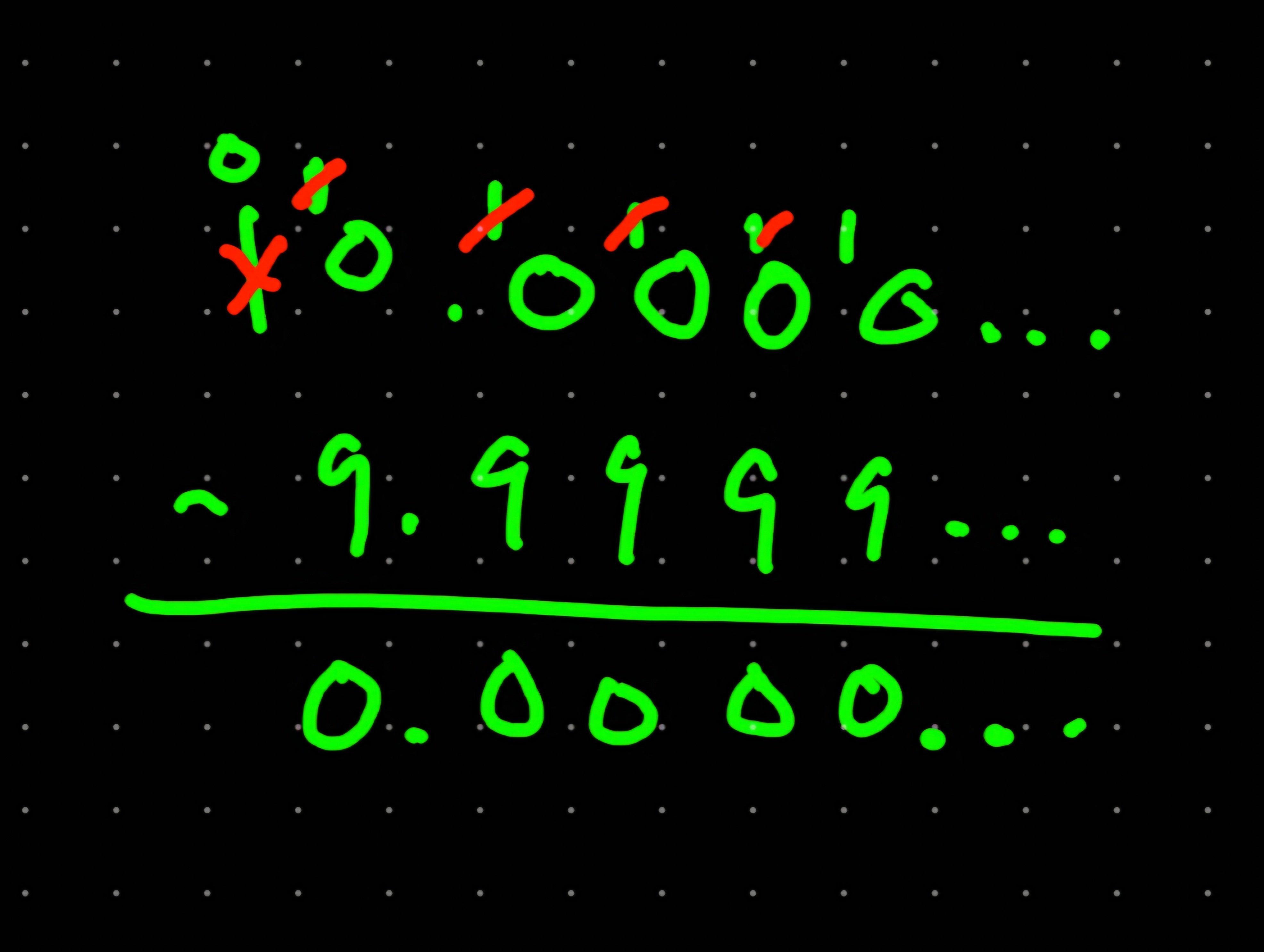
If they don't get it and keep trying to show you how you are wrong they will at least be out of your hair until forever.
You don't subtract from 10, but from 10x0.999.... I mean your statement is also true but it just proves the point further.
If they aren't equal, there should be a number in between that separates them. Between 0.1 and 0.2 i can come up with 0.15. Between 0.1 and 0.15 is 0.125. You can keep going, but if the numbers are equal, there is nothing in between. There's no gap between 0.1 and 0.1, so they are equal.
What number comes between 0.999... and 1?
(I used to think it was imprecise representations too, but this is how it made sense to me :)
THAT'S EXACTLY WHAT I SAID.
I thought the muscular guys were supposed to be right in these memes.
He is right. 1 approximates 1 to any accuracy you like.
Is it true to say that two numbers that are equal are also approximately equal?
I recall an anecdote about a mathematician being asked to clarify precisely what he meant by "a close approximation to three". After thinking for a moment, he replied "any real number other than three".
"Approximately equal" is just a superset of "equal" that also includes values "acceptably close" (using whatever definition you set for acceptable).
Unless you say something like:
a ≈ b ∧ a ≠ b
which implies a is close to b but not exactly equal to b, it's safe to presume that a ≈ b includes the possibility that a = b.
If 0.999… < 1, then that must mean there’s an infinite amount of real numbers between 0.999… and 1. Can you name a single one of these?
Remember when US politicians argued about declaring Pi to 3?
Would have been funny seeing the world go boink in about a week.
To everyone who might not have heard about that before: It was an attempt to introduce it as a bill in Indiana:
https://en.m.wikipedia.org/w/index.php?title=Indiana_pi_bill
the bill's language and topic caused confusion; a member proposed that it be referred to the Finance Committee, but the Speaker accepted another member's recommendation to refer the bill to the Committee on Swamplands, where the bill could "find a deserved grave".
An assemblyman handed him the bill, offering to introduce him to the genius who wrote it. He declined, saying that he already met as many crazy people as he cared to.
I hope medicine in 1897 was up to the treatment of these burns.
This is why we can't have nice things like dependable protection from fall damage while riding a boat in Minecraft.
Reals are just point cores of dressed Cauchy sequences of naturals (think of it as a continually constructed set of narrowing intervals "homing in" on the real being constructed). The intervals shrink at the same rate generally.
1!=0.999 iff we can find an n, such that the intervals no longer overlap at that n. This would imply a layer of absolute infinite thinness has to exist, and so we have reached a contradiction as it would have to have a width smaller than every positive real (there is no smallest real >0).
Therefore 0.999...=1.
However, we can argue that 1 is not identity to 0.999... quite easily as they are not the same thing.
This does argue that this only works in an extensional setting (which is the norm for most mathematics).
Are we still doing this 0.999.. thing? Why, is it that attractive?
The rules of decimal notation don't sipport infinite decimals properly. In order for a 9 to roll over into a 10, the next smallest decimal needs to roll over first, therefore an infinite string of anything will never resolve the needed discrete increment.
Thus, all arguments that 0.999... = 1 must use algebra, limits, or some other logic beyond decimal notation. I consider this a bug with decimals, and 0.999... = 1 to be a workaround.
don't sipport infinite decimals properly
Please explain this in a way that makes sense to me (I'm an algebraist). I don't know what it would mean for infinite decimals to be supported "properly" or "improperly". Furthermore, I'm not aware of any arguments worth taking seriously that don't use logic, so I'm wondering why that's a criticism of the notation.
People generally find it odd and unintuitive that it's possible to use decimal notation to represent 1 as .9~ and so this particular thing will never go away. When I was in HS I wowed some of my teachers by doing proofs on the subject, and every so often I see it online. This will continue to be an interesting fact for as long as decimal is used as a canonical notation.
Meh, close enough.
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.
Rules
